Curso de electrónica. Aprenda tecnología digital VII

COMPUERTAS LÓGICAS

Como una introducción  a las compuertas lógicas , diremos , que es una simbología real de las operaciones de : Suma y Multiplicación ( Unión , Intersección ) lógicas , con sus respectivas ecuaciones  y tablas de verdad , necesarias para diseñar circuitos digitales
Los pasos a seguir son:

1. Traducir el problema a una tabla de verdad
2. Extraer de La tabla de verdad la función lógica de forma de Mini términos
3. Simplificar la función  con el método más oportunos
4. Construir el circuito con los dispositivos más adecuados.

La ecuación de un circuito lógico se puede realizar con lógica de contactos, diodos, transistores. Sin embargo lo más práctico y fiable es la utilización de compuertas lógicas Integradas, construidas con tecnología SSI (Integración a Media Escala).
Existen un amplio número de compuertas clasificada por Familias, las cuales presentan  distintas características, dependiendo de la tecnología con la que están constituidas.
Son muchas las tecnologías de fabricación  de circuitos digitales integrados, sin embargo, nos referiremos a dos familias principalmente que son: Familias TTL ( Lógica transistor – Transistor) y la familia CMOS, en este caso se utiliza un transistor MOS (Metal – Oxido- Semiconductor)

Familia Lógica  TTL

Estas compuertas están constituidas mediante resistencia, diodos y transistores bipolares,
Esta familia es la más popular  debido a su bajo costo y gran variedad de circuitos que se han desarrollado por la totalidad de los fabricantes de Semiconductores.
La Familia TTL comprende de varias serie que han sido desarrollados progresivamente para mejorar algunas de las características de los fabricantes anteriormente.
La primera serie fue la TTL Standard conocido como la serie  54 / 74. Cuyas características son:

1. Tensión de Alimentación comprendidas entre : 4 , 5 y 5, 5 (v)
2. Temperatura de trabajo : 0  a  70 ºc
3. Disipación de Potencia  :  10 mili – Watts
4. Tiempo de Propagación medio : 10 mili seg

La serie 54 presenta las mismas características, la diferencia es la T º de trabajo, que en este caso está comprendida entre: - 55 º c  y  +125 º c , su precio es más elevado.
La serie 54 / 74 S  ( S chttky), mejora el tiempo de conmutación, 3 nano segundo, disipación de potencia por función  por función es 10 mili watts.

La serie 54 / 74 LS (Low – Power – Schottky), cuya potencia por función es 2 mili Watts y tiempo de conmutación, 5 nano segundo.
La serie  54 / 74 F ( Fast), con una disipación por función de 4 mili-watts y tiempo de propagación de 3 nano segundo.

Familia  Lógica  CMOS

Los circuitos integrados de la familia  CMOS  ofrecen una fuerte competencia a las de Tecnología TTL, debido a las mejores características que presentan en algún aspecto. La principal la menos disipación de potencia por función, la que se supone una mayor densidad de integración. Por otro lado esta familia  tiene una mayor inmunidad al ruido eléctrico que la familia TTL. Por el contrario, los tiempos de propagación, en general son superiores.
La tecnología CMOS es la síntesis de otras dos familias que utilizan el transistor MOS como elemento básico. Estos son los NMOS, constituidos por transistor de canal N, los PMOS cuyo elemento fundamentalmente es el transistor  transistor  MOS de Canal P .
La letra  C  que es parte de la sigla  C MOS es la abreviatura de COS (Simetría Complementaria).
Las características más importantes de la Familia C MOS  en general son:

1. Tensión de alimentación entre : 3  y  18  volts
2. Rango de Temperatura de trabajo :  - 40 º c      y     + 85  º c
3. Gran Inmunidad al ruido eléctrico
4. Potencia disipada por puerta es 10  nano Watts

La familia  C MOS  básica aparece en el catálogo como la serie 4000
Clasificación de compuertas Básicas

  Obtener la Ecuación Lógica de una  Tabla de  Verdad (T. de V.)

   Dada la siguiente T de V que representa la condición de un determinado problema
   Obtener :

1. La ecuación Booleana en Mini términos
2. La ecuación Booleana en Maxi términos

    

a	b	c	Y
0	0	0	0	. . . .
0	0	1	1	a b  c
0	1	0	1	a  b  c
0	1	1	0	. .  . .
1	0	0	1	a  b  c
	0	1	0
1	1	0	0
1	1	1	1	a  b  c

Para obtener dicha función se observan todas las salidas que están en nivel alto ( 1 lógico). Se multiplican todas las variables de esa fila, en este caso son  4, que indica en la tabla, en la primera columna de la derecha, ahora  sumamos  estos términos, como se indica en la siguiente ecuación.

..  ..          ..      ..          ..   ..

F( a,b,c) = a  b  c  +  a  b  c  +  a  b  c  +  a  b  c

Para obtener la función en Maxitérminos, ahora  se observan las salidas de la  T de  V que estén en nivel bajo (0 lógico). Se niega cada variable por separado y se suman por cada  fila por  separado, ahora bien estos cuatro términos se multiplican, quedando como se indica en la ecuación.
                                                                  ..       ..        ..               ..      ..      ..
                          F (a,b,c) = (a  +  b  +  c) * ( a  +  b  +  c)  *  (a  +  b  +  c) * (a  +  b  +  c)

  Ejemplo ( 3  )

  A partir de la siguiente T de  V , se pide
    a) Obtener la ecuación  lógica  en mini términos
    b) Simplificar la ecuación
    c) Implementar el circuito con compuertas lógicas

a      b       Y

Tabla de Verdad                       0     0       0

0     1       1

1     0       1

1     1       0

                                                                                     ..                   ..
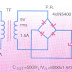
  Aplicando procedimiento anterior, se tiene :    Y  =  a    b   +   a   b   +   a  b
Sin simplificar la ecuación, el circuito queda de la siguiente forma:

           
   Simplificando la ecuación, aplicando el método de Karnaugh en dos variable

       La ecuación en Maxiterminos se puede transformar en minitérminos se tiene:
                               ..      ..
   Y = ( a  *  b ) + ( a  *  b ) 
                               ..      ..
             ..     ..         ..      ..
   Y = ( a  *  b ) + ( a  *  b ) 

            .                            .  
                                ..     ..
             ..      ..         ..     ..
    Y = ( a  *  b ) + ( a  *  b )
             .                           .
             ..      ..
    Y = ( a  *  b ) + ( a  *  b )   
 

La implementación del circuito con las compuertas adecuadas corresponde a :

                        

Se puede concluir que cuando se diseña un circuito a partir de una T de V, siempre se obtiene la ecuación lógica, con la menor cantidad de términos, los que pueden ser, mini términos o maxi términos, esto se logra observando las salidas de la T de V. Si hay una menor cantidad de 1 lógicos se trabaja con  mini términos, de lo contrario se traba en función de maxi términos.

  Ejemplo (4)

Para la tabla de verdad de la función  AND. Se pide obtener:

a        b       Y

0       0        0

0       1        0

1       0        0

1       1        1

1. Obtener la ecuación lógica del circuito en función de mini términos y maxi términos
2. Implementar el circuito con compuertas lógicas para ambos casos

Desarrollo

a) La ecuación del circuito en mini términos es:     Y  =  a  *   b
b) La implementación del circuito es:
                                                                    

1. Usando  maxi términos sin simplificar la ecuación es :

..         ..

S = ( a  +  b ) * ( a  +  b ) * ( a  +  b )

  La implementación del circuito lógico es:
                                            
Transformar  la ecuación de mini términos en maxi términos se tiene:
                            ..       ..
Y = a * b   +  a * b   +  a * b
                             ..       ..
       ..    ..        ..    ..       ..    ..
Y = a * b   +   a * b  +   a * b   
       .                                    .     
                            ..       ..
       ..    ..       ..    ..       ..    ..
Y = a * b  +   a * b  +   a * b  
       .                                   .
        ..    ..      ..                  ..
Y =  a * b  +  a * b  +  a * b

 El circuito implementado con función en maxi términos es:
                                                                

  CIRCUITOS  COMPARADORES

Son circuitos que permiten comparar palabras binarias de uno  ó más bits. Se pueden realizar los circuitos con compuertas básicas o con circuitos integrados. El circuito integrado utilizado para estos fines es el CI 7485, que es un comparador de  palabra de 4 bits.
Análisis de un circuito con compuertas básicas, se comparan dos palabras  a  y  b   de un bits cada una.
La tabla de verdad es la siguiente:
                                  

entradas		S1	S2	S3
a	b	a = b	a > b	a < b
0	0	1		-
0	1	-	-	1
1	0	-	1	-
1	1	1		-

  Las ecuaciones lógicas son:
            ..     ..
  S1 =  a  *  b  +  a  *  b
                   ..
  S2  =  a *  b
             .. 
  S 3  =  a  *  b

  Implementación del circuito con compuertas básicas

 COMPARADOR   7885

Es un comparador de palabras de 4 bits cada palabra. Este circuito integrado se puede conectar de forma de comparar palabras de 8 bits.

DECODIFICADORES

Son circuitos que tienen la habilidad de seleccionar una determinada salida  dependiendo de las combinaciones binarias en su entrada.

  Análisis para un Circuito Decodificador de dos Entradas y cuatro Salidas.
  Diseñar la tabla de verdad.
       

Entradas		Salidas
a1	a 0	S3	S2	S1	S0
0	0	1	1	1	0
0	1	1	1	0	1
1	0	1	0	1	1
1	1	0	1	1	1

La tabla de verdad se activa con un nivel bajo (0 lógico).
Por ejemplo cuando, las entradas  a 1 y  a 0  están en  0 lógico, se activa la salida S0, significa que lleva a tierra un terminal de ese circuito, por lo tanto el otro extremo de esa carga o circuito debe estar a + V, para que quede alimentado y se active.
Las ecuaciones lógicas del circuito en Maxi términos obtiene de la Tabla de Verdad

 Se implementará el circuito con las ecuaciones de maxi términos

       

Existen Decodificadores como circuitos integrados, como por ejemplo 74 L S 42
tiene 4 líneas de entrada y 10 líneas de salidas, aplicando una combinación BCD a su entrada, se activa la correspondiente línea de salida.

DECODIFICADOR   BCD  A   SIETE   SEGMENTOS

Una forma  usual de  representar un número binario en un número decimal es utilizar  un decodificador de siete segmentos y activar una pantalla de siete segmentos, los segmentos se indican con las letras : a , b ,c ,d , e ,f , g  . Con dichos segmentos se pueden representar los números : 0 , 1 , 2 , 3 , 4 , 5 , 5 , 6 , 7, 8 , 9 . Un decodificador comercial es el CI 7447, en la figura se indica la ubicación de los terminales para realizar una conexión, la entrada corresponde a la combinación binaria y las salidas que deben ir al Display de 7 segmentos en ánodo común

  GENERADOR DE PULSOS CON EL C I  555
               (Circuito Oscilador)

El C I 555, es un circuito que tiene una variada clase de aplicaciones, dentro de las cuales esta la aplicación de poder generar un tren de pulsos, también llamado circuito oscilador, en esta oportunidad no se analizará al interior de dicho CI, mas bien
nos abocaremos a  reconocer la ubicación de  sus terminales, su función en forma general, pero  en forma específica  diseñar  y armar el circuito. Como también, la observación de las formas de onda más importante para reconocer el buen funcionamiento del circuito.

            CIRCUITO DE APLICACIÓN

E l condensador  C*, es un condensador que se conecta entre el pin 5 y  el común  su utilización es para eliminar señales de ruido eléctrico cuando la situación lo aconseja, el valor de 0,01 µF, lo entrega el fabricante.

         Las ecuaciones básicas del circuito son:

La frecuencia de salida, esta dada por :  f  =  1 ,443 / [(Ra  +  2 Rb)*Ct]
                                                      
La relación de la frecuencia y el Periodo esta dada por :    f = 1 /  T

El periodo (T), esta dado por la suma de  t 1 ( tiempo de carga del condensador) y  t 2 tiempo de descarga del condensador, o sea :

                                                         T =   t 1  +  t 2

   t 1  =  0,693 ( R a  +  R b ) * C t

   t 2  =  0,693 * R b * C t

   T =  t 1  +  t 2  =  0,693 ( R a + R b)*Ct  +  0,693 * Rb *Ct

  Trabajando la ecuación algebraicamente es tiene la siguiente solución:

  T  =  0,693 * (  Ra   + 2 *R b ) * Ct

  T =  1 /  f

El Tiempo Útil (D), se define como la relación  de tiempo alto (t 1) y el periodo (T), esta razón esta dada normalmente en tanto por ciento (%)

                            D (%) =  t1 / ( t1 + t2 )   =    t 1 /  T

Diseñar un circuito oscilador  para tener una señal de 200 (hz), D = 60 % y un condensador de 0,47 µ F.
Con los datos dados se puede conocer el periodo (T).  T = 1/ f =
1 / 200 = 5 seg.)

El tiempo de t1, corresponde al 60% del periodo:  t1 = 5 (mseg) * 0,6) =
 3 (mseg)

Por diferencia se puede conocer, el tiempo de descarga, t2 = T – t1 =
2 (mseg)

T2 = 0,693 * Rb * Ct, despejando Rb, se tiene:

         Rb =  t 2 / ( 0,693 * 0,47 * 10 -6 ) = 6 ,14  K Ω

 De la ecuación de, t 1, despejando se tiene:

       R a + R b =  3 * 10 -3 / ( 0,693 * 0,47 *10 -6 )  = 9 , 21 KΩ

        R a =  9 , 21 kΩ -  6, 14 K Ω  =  3 ,07 KΩ

  Formas de onda del condensador de carga  y  señal de salida.