Curso de electrónica. Aprenda tecnología digital IV

GUIA DE AMPLIFICADORES OPERACIONALES

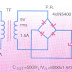
Para desarrollar los siguientes los problemas haga uso del circuito de la Fig. ( 1 )
Fig. Nº1
Prob. Nº 1

Si  R1 = 10  Kohm , R2 = 33 Kohm , Vi = 2.5 ( V) . Se pide calcular
a) La ganancia de tensión del circuito.                       Rpta: 3.3

b) La tensión de salida, Vo                                        Rpta : - 8. 25 ( V)

Prob. Nº 2

Si la ganancia de tensión del circuito es igual a 10 . Diseñe el circuito de la Fig.(1)
Rpta :  R1 = 1 Kohm ;  R2 = 10 K ohm

Prob. Nº 3

Si la señal de entrada es una señal senoidal, como se indica a partir de ella graficar
la tensión de salida, Vo  .

Prob. Nº 4
Para el circuito de la Fig. Nº 2 , se pide calcular la tensión de salida , Vo
Fig. Nº 2
    Rpta: 10.77 ( v)

Los siguientes problemas se desarrollan, tomando en cuenta el circuito de la Fig (3)
Fig. Nº 3

Prob Nº 1

¿Que nombre recibe el circuito de la figura nº 3 ?

Prob Nº 2

S i  R1 = 2.2 K ohm , R2 = 15 K ohm , Vi = 3 (v) ,  +V cc = 15 (v)  ,  - Vcc = 15 (v)
Calcular la ganancia del circuito                  Rpta :  7. 82

Prob Nº 3

Calcular la tensión de salida, Vo.                              Rpta : 23 , 46 (V)

Prob Nº4

¿Existe saturación de tensión de salida? Justifique la respuesta.

Prob Nº 5

Si la ganancia de tensión del circuito  es igual a 8, diseñar el circuito, si R1 = 10 K ohm.

Rpta:    R1 = 10 K ohm  ,  R2 = 70 K ohm .

Si la tensión de salida es igual a 5. 5 (v). Calcular la tensión de entrada, Vi

Rpta : 688 ( mv)

Prob Nº 5

Si la tensión de entrada es senoidal , graficar la tensión de salida , Vo

Utilizar el circuito de la fig Nº 4 , para responder las siguientes preguntas.
 Fig. Nº 4

Preg Nº1

Si , V1= 1(v) , V2 = - 2 (V) , V3 = 3(V) ;  R1 = R2 = R3 = 10 K ohm  , R4 = 22 K ohm
Calcular la tensión de salida , Vo

Rpta : - 4. 4 ( v)

Preg Nº 2

Si , V1 = 1, 5 (v) ; V2= 800 mv ; V3 =1, 8 (v) ;   R1 = 1,5 Kohm .  R2 = 2 , 2 K ohm
R3 = 3 ,3 K ohm . Calcular Vo.                                        Rpta : 7. 8 (v)

Preg Nº 3

Calcular la corriente  It = I1+I2+I3  del circuito.                                Rpta :  2. 36 ( ma)

Para el circuito de la Fig. (5), responda las siguientes preguntas
Fig. Nº 5
Prob Nº1

Si  R1 = R2 = 5 K ohm ; R3 = R4 = 15 Kohm

1. Calcular la tensión de salida , Vo
2. Calcular la corriente , I3
3. Calcular la tensión , Vb

Rpta:  a)  - 6, 6 (v)   ;  b) 0,22 ( ma)  ;  c)  - 3,3(v)

Prob Nº2

Si  R1 = 1, 5 Kohm ;  R2 = 1 Kohm ; R3 = 10 K ohm ; R4 = 6,8 Kohm

1. Calcular la tensión de salida , Vo

b)   Calcular la tensión en el punto “b”

Rpta:   a)         (v)  ;        b)           (v)

Para el circuito de la fig. (6) , responda las siguientes preguntas
 Fig. Nº 6

Prob Nº1

Si Rc y  Re  son iguales a 5 Kohm , hfe = 80 , hie = 1 Kohm. Las señales aplicadas a las
entradas (base de cada transistor) son:  V1 = 520 (mv) ,  V2= 480 (mv). Se pide calcular:

1. Ganancia a modo común (Ac)
2. Ganancia diferencial ( Ad)
3. Relación de Rechazo a Modo Común (RRMC)
4. Tensión a modo común (vc)
5. Tensión diferencial (vd)
6. La tensión de salida ( v 2)

Rpta: a) 0,5   ;  b) 200   ;  c) 400  ;  d)  500 mv   ;  e) 40 mv   ;  f) 8250 mv

Prob Nº2

Si la RRMC , aumenta a 4000 , manteniéndose la Ad  en 200 , se pide

a) La ganancia a modo común (Ac)
b)La tensión de salida v2

Rpta: a) 0,05      ;     b) 8025 mv

Prob Nº3

En cual de las dos situaciones: Prob. (1)  o  Prob. (2), el amplificador diferencial tiene mejores características. Justifique la respuesta

Utilizando el circuito de la fig (7), desarrolle los siguientes problemas
Fig. Nº 7
Prob Nº1

Si E = 10 (v) ,  R1 = 2,2  K ohm , R2 = 6,8 K ohm  ,  +V = 12 (v)  ,  -V = -12 (v) . Vi es
una señal alterna de valor máximo igual  5 (v) . Se pide:

1. Graficar la señal de entrada y salida en función del tiempo, agregar valores en los puntos adecuados.
2. Graficar la característica de transferencia

Prob Nº2

Si  E = - 10 (v)  ,  R1 = 5,8 (v)  ,  R2 = 5,6 (v) ,  + V = 10 (v)  ,   - V = - 10 (v). Si Vi
es una señal alterna de valor máximo igual a 6 (v).Se pide:

1. Responda las preguntas del Prob(1).

Prob Nº3

Si E = 12 (v)  ,  R1 =  R2 = 5 K ohm , +V = 12 (v)  ,  - V = -12 (v) . Si  Vi es una señal
alterna de valor máximo  3 (v). Se pide:

1. Responda las preguntas anteriores

Desarrolle los siguientes ejercicios, haciendo uso del  circuito Fig. ( 8).
       Fig. Nº 8

Prob Nº1

Si  E = 6 (v) , R1 = 1 K ohm ,  R2 = 2 K ohm , +V = 12 (v) , - V = - 12 (v) . Si Vi es una
señal alterna de valor 5 (v) de valor igual a 5(v) medida con respecto del común. Se pide

1. Responda las preguntas anteriores

Prob Nº2

Si  E = - 9 (v) ,  R1 = 2,2 K ohm ,  R2 = 3,7 K ohm , +V= 15 (v) , -V = -15 (v) . Si  Vi es una señal alterna de valor máximo igual a 10 (v). Se pide

1. Responda las preguntas anteriores

Prob Nº3

Si  E = 10 (v) ,  R1 = 5 K ohm ,  R2 = 10  K ohm ,  +V = 15 (v) ,  - V = -15 (v) .Si Vi
es un señal alterna de valor máximo igual a 6 (v) . Se pide

1. Responda las preguntas anteriores

Desarrolle los siguientes ejercicios utilizando el  circuito de la fig. ( 9 ).

 Fig . Nº 9
Prob Nº1

Si  R1 = 5 K ohm ,   R2 = 10 K ohm ,  +V = 12 (v) ,   - V = - 12 (v) . Si Vi es una
señal alterna de valor máximo igual a 8 (v) . Se pide

1. Graficar las formas de ondas de entrada y salida en función del tiempo
2. Graficar la característica de transferencia.
3. Mida la tensión de Histéresis

Obs: Agregar los valores correspondientes en los gráficos.

Prob Nº2

Si R1 = 6,8 K ohm , R2 = 8 K ohm , + V = 15 (v)  ,  - V = 15 (v) . Si Vi es una señal
alterna de valor máximo igual a 10 (v). Se pide

a) Responda las preguntas del problema anterior

Prob Nº 3

Si  R1 = 2 K ohm ,   R2 = 4 K ohm ,  +V = 9 (V) ,   - V = - 9 (v) . Si Vi es una señal
alterna de valor máximo igual a 7 (v) . Se pide :

1. Graficar las señales de entrada y salida en función del tiempo.
2. Graficar la característica de transferencia.
3. ¿ Cual es  el valor mínimo de Vi  de entrada para que la señal de salida cam-

bie de estado positivo al estado negativo.

PROB Nº4

Para el circuito de la figura (10), si  Vcc = +12 (v),  Vcc = -12 (v), Vt = 10 (v)
Ra = 2 K ohm  ,  Rb = 4 K ohm . La tensión de entrada Vi es una tensión alterna cuyo
valor máximo es de 15 (v), se pide:

1. Determinar los valores V1 y V2 que producen los cambios de tensión en la salida ,Vo
2. Graficar la forma de onda Vo en función del tiempo
3. Graficar la característica de transferencia ( Vi , Vo)
4. Determinar la tensión de histéresis

Rptas:  a) V1 = 3, 17 (V)  ; V2 = 10,17 (v)         d) V h = 7 (v)

SISTEMAS  NUMERICOS

INTRODUCCION

Todos conocemos el Sistema Decimal , que utiliza los símbolos: 0,1,2,3,4,5,6,7,8,9 . El sistema decimal entrega un valor de posición característico. Consideremos el número 238. El número 8 esta en la posición de las unidades, el número 3 en la posición de las decenas y el 2 en la posición de las centenas.
  Las 8 unidades, valor posicional  mínimo
  Las 3 decenas corresponden a 30 unidades
  Las2 centenas corresponden 20 decenas y 200 unidades
  Sumando se tiene : 200 + 30+ 8 , se tiene un número decimal igual a 238.
El sistema decimal, también se llama sistema de base 10, ya que tiene 10 símbolo diferentes.
El número 238, utilizando la base 10, también se puede representar como la serie:

   238  =…….. 2* 102 + 3* 101 + 3* 100

El sistema decimal es el sistema numérico utilizado por las personas en su vida cotidiana. Pero no es el único sistema numérico que existe. También existen entre otros:
Hexadecimal , el cual tiene 16 símbolos , que son: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F también conocido como sistema numérico base 16.
Por último esta el sistema binario, el cual tiene dos símbolos para representar las cifras, que son: 1 ,0. Este último Sistema se conoce como lenguaje de Máquina debido, por que es el lenguaje que ocupan, por ejemplo los computadores para realizar todas sus operaciones internas desde el control hasta el sistema de cómputo.
Existen otros sistemas numéricos, pero los más representativos son los que se han indicado.
La siguiente tabla indica la equivalencia entre los números: Decimal, Binario y el Hexadecimal

Decimal	Binario	Hexadecimal
0	.  0000	0
1	.  0001	1
2	.  0010	2
3	.  0011	3
4	.  0100	4
5	.  0101	5
6	.  0110	6
7	.  0111	7
8	.  1000	8
9	.  1001	9
10	.  1010	A
11	.  1011	B
12	.  1100	C
13	.  1101	D
14	.  1110	E
15	.  1111	F
	Tabla fig 1

  De la tabla de la fig (1)

  E l numero decimal 5 equivale al número binario 0101
  El número decimal  11 equivale al número hexadecimal  B

Convertir un Número Binario a Decimal

Binario              1  0  0  1  1

Decimal        1 * 2 4 + 0 * 2 3  + 0 * 22 +1 * 21 + 1 * 2 0

                       16      +     0      +    0     +    2     +    1
  
      Por lo tanto el valor es 19

  L a forma de representar la operación es:

       10011 2      equivale a    19 10

Convertir un Numero Decimal a Binario

             Se utiliza el método de división sucesiva por  2.  Convertir  el Decimal 19 a un equivalente en Binario

  19  :    2   =   9        , el resto es  1
   1

Se toma el cuociente y se divide por 2

  9  :    2   =  4      ,   el resto es    1
  1

Se continúa con el proceso

  4  :   2   =   2     ,     el resto es    0 
   0

   2  :  2  =  1    ,        el resto es   01
   0

  1  :  2   =  0   ,        el resto es    1
  1

El número binario se construye, haciendo una serie con los restos de cada división, donde la posición más significativa  de la cifra corresponde al número originado por la última división, por lo tanto se tiene como resultado:

                     19 10       equivale a     10011 2

Convertir   Hexadecimal  a   Decimal

En este caso se utiliza una serie uso de la base  16.

Convertir                 2 B 6  16      equivale a      X  10

 2  B  6    equivale a   2  *16 2  +  B * 16 1  + 6  * 16 0

                                  2  * 256  +  11 * 16   + 6 * 1
   
                                  512         +    176     +   6
                                 
                                    694

Por lo tanto:   2  B  6 16  equivale  a      694 10

Convertir Decimal a Hexadecimal

Un método es división sucesiva por la base  16, método similar al utilizado cuando se trabajó en la conversión de Decimal a Binario

Convertir    45  10  a su  equivalencia en   X  16

  45  :  16  =  2     , resto   R o  = 13      ;      D =  13
  13

  2  :  16  =  0      ,  resto   R 1  =  2 
  2

                  45 10      equivale   a  2 D 16    

Convertir  Hexadecimal   a   Binario

En este caso, cada símbolo de la cifra  Hexadecimal se reemplaza por un grupo de 4 bits.
 Convertir   1 A 16      equivale    a    X 2

   1   equivale a  0001              ;         A  equivale a  1010

   1 A 16     equivale  a      00011010 2

Convertir Binario  a   Hexadecimal

Se reúnen grupos de 4 BIT de derecha a la izquierda, donde cada grupo corresponde al equivalente a un numero Hexadecimal

  Convertir    11010011 2   equivalente a    X 16

1. equivale a  D
2.      equivale a  3

11010011 2   equivale a   D3 16

                   CODIGOS

Cualquier información que se desea, procesar, almacenar mediante un sistema digitales, deberá ser traducida o codificada en un tipo de lenguaje apropiado. La forma correcta de hacerlo es convertir número, signo, instrucción u operación en un conjunto de señales eléctricas digitales que será diferente en cada caso. Cada una de estos datos estará constituida por una serie de unos y ceros que indicará niveles altos y bajos de tensión respectivamente. Algunos de estos códigos son: BCD, GRAY y ASCII
Por ejemplo el número decimal  9, podrá ser codificado en BCD  por  1001.El 1,0 se conocen como un Bit.
La tabla de la Fig.(2), representa la codificación de un número decimal  en Código GRAY

DECIMAL                                          GRAY
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000

   
CODIGO   ASCII

Es un código Alfanumérico (American   Standard  Code  For  Información Inter- change). Existen códigos de 6 y 7 bits. Permite representar cifras decimales, caracteres alfabéticos, signos especiales y diversas órdenes de control para periféricos como Impresoras, Pantallas, etc.

Formato        P   b 7   b 6  b 5   b 4  b 3 b2  b1

b 7  : Representa el BIT de mayor peso o mas significativo
P   : Representa el BIT  de paridad

Utilizando la tabla de la figura (3), representar la letra  A  en código ASCII

    A   equivale a    1000001

  La instrucción  SUB , equivale a   0011010 en código ASCII

ARITMETICA  

Suma y Resta Binaria .Para realizar dichas operaciones se aplica el mismo algoritmo que es aplica cuando se opera con el sistema decimal.

 SUMA

También es posible aplicar la siguiente tabla que resume los pasos básicos de esta operación. Para sumar dos números de un BIT cada uno.

A             B              Suma    Reserva
0              0                 0             0
0              1                 1             0
1              0                 1             0
1              1                 0             1
Realizar la siguiente suma
0     1  0  0                                        1   1   1   1   1
+     0    1  0  1                                   +   1    1  0    0   1
1    0   0  1                                    1  1   0   1   0    0

Complemento de un Número

  Los complementos típicos de un número son:
       Complemento a uno
       Complemento a dos

El complemento a uno de un número se obtiene con solo cambiar los unos por cero y los ceros por unos de una cifra binaria.
Si el número binario es  1 1 0 1 0 1   el complemento a uno es     0  0  1 0 1  0
El complemento a dos de un número binario se puede realizar al menos de dos formas:
     Método Nº1
Obtener el complemento a uno del número binario y se le suma un uno en la posición del BIT menos significativo.
     Método Nº 2
Al número binario en cuestión, se repite la cifra de derecha hacia la izquierda hasta el primer uno que encuentra y a continuación  se continua con complemento a uno.
 Obtener el complemento a dos de :   0  1  0  1  1

1º   Complemento a uno:    1  0  1  0  0

2º   Sumarle un uno        :     1  0  1  0  0

+                      1

1    0  1  0  1

El  segundo método se aplica la definición en forma directa y el resultado se obtiene en  menor tiempo.

Los complementos se utilizan para realizar las restas de números binarios, llevando la resta a una suma de números, por lo tanto se aplica siempre un solo procedimiento independiente, si se trata de una suma o resta de números binarios.

RESTA BINARIA

Aplicando procedimiento, explicado anteriormente se desarrolla el siguiente ejemplo

0  1  0      (minuendo) -  0    1  1  1     ( sustraendo)                         ( resultado   )

1º    Se toma el sustraendo, y se  hace el complemento a dos, es resultado parcial es

1   0  0  1

2º    Ahora, se realiza la suma entre el minuendo y el sustraendo complementado

1  0  1  0

+ 1  0  0  1

3º   El resultado  de la suma es  :      1   0  0  1  1

E l rebalse del  5º  BIT, indica  el signo del  resultado.
Si es  1   , el resultado es positivo.
Si es  0   , el número es negativo. Pero el resultado final se obtiene complementando el resultado parcial.